Диагональ правильного шестиугольника формула
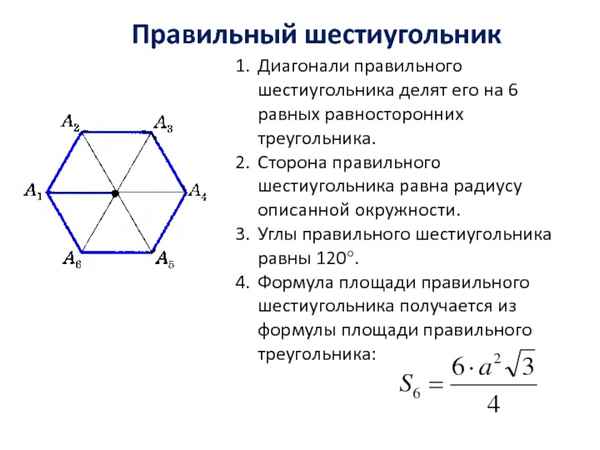
Правильный шестиугольник
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Обучающее видео
БЕСПЛАТНО
Техническая поддержка:
help@ege-study.ru (круглосуточно)
Пробные репетиционные ЕГЭ: пройдите бесплатное тестирование! Все, как на настоящем ЕГЭ.
Звоните, чтобы записаться:
8 (495) 984-09-27 или 8 (800) 775-06-82
Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная пpaктика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.
Все поля обязательны для заполнения
Премиум
Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.
Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.
- Уравнения (задача 13)
- Стереометрия (задача 14)
- Неравенства (задача 15)
- Геометрия (задача 16)
- Финансовая математика (задача 17)
- Параметры (задача 18)
- Нестандартная задача на числа и их свойства (задача 19).
Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.
Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.
Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие прострaнcтвенного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.
Как пользоваться?
- Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
- Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
- Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
- Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
- Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.
Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.
Свойство диагоналей правильного шестиугольника
Правильным шестиугольником называется выпуклый многоугольник с шестью одинаковыми сторонами и шестью углами.
Внутренние углы в правильном шестиугольнике равны (120^circ):
(alpha = 120^circ)
Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac >
ormalsize)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)
Периметр правильного шестиугольника
(P = 6a)
Площадь правильного шестиугольника
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник хаpaктеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Читать еще: Как правильно сматывать кабельФормулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
Ответ. V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильный многоугольник
Правильный многоугольник — это многоугольник, все стороны и углы которого равны.
Вокруг правильного многоугольника можно описать окружность и в него можно вписать окружность. Центры этих окружностей совпадают.
Правильный шестиугольник
Правильный шестиугольник – это шестиугольник, все стороны и углы которого равны.
Описанный многоугольник
Если все стороны многоугольника касаются некоторой окружности , то он называется описанным многоугольником .
Диагональ правильного шестиугольника формула
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
cdot a^2> > , где a — сторона шестиугольника.
Через радиус вписанной окружности
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
cdot r^2> , где r — радиус вписанной окружности.
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
cdot R^2> > , где R — радиус описанной окружности.
Интересные факты
Форму правильного шестиугольника имеют пчелиные соты, сечение гаек и карандашей, кристаллическая решетка графита.
Шестиугольник — это многоугольник, общее количество углов (вершин) которого равно шести.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Чему равна сумма углов выпуклого шестиугольника?
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов. См. теорему о сумме углов многоугольника.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Правильный шестиугольник
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- всі внутрішні кути рівні між собою
- кожен внутрішній кут правильного шестикутника дорівнює 120 градусам
- всі сторони рівні між собою сторона правильного шестикутника дорівнює радіусу описаного кола
- правильний шестикутник заповнює плоскість без пропусків і накладень
Формулы для правильного шестиугольника
(по порядку следования формул)
- Радиус описанной окружности (R) правильного шестиугольника равен его стороне (t)
- Все внутренние углы равны 120 градусам
- Радиус вписанной окружности (r) равен корню из трех, деленному на два и умноженному на длину стороны t (радиус описанной окружности R)
- Периметр правильного шестиугольника (P) равен шести радиусам описанной окружности (R) или четыре корня из трех, умноженным на радиус вписанной окружности (r)
- Площадь правильного шестиугольника равна трем корням из трех пополам, умноженным на квадрат радиуса описанной окружности (R) или квадрат стороны (t); либо площадь правильного шестиугольника равна двум корням из трех, умноженным на квадрат радиуса вписанной окружности (t)
Задача
Найти объем цилиндра, вписанного в правильную шестиугольную призму, каждое ребро которой равно t .
Решение.
Так как высота цилиндра Н равна высоте призмы и равна а, достаточно найти радиус основания цилиндра, который будет равен радиусу окружности, вписанной в правильный шестиугольник.
Знайти об’єм циліндра, вписаного в правильну шестикутну призму, кожне ребро якої дорівнює t .
Рiшення.
Так як висота циліндра Н дорівнює висоті призми і дорівнює а, достатньо знайти радіус основи циліндра, який буде дорівнювати радіусу кола, вписаного в правильний шестикутник.
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Правильный шестиугольник
Правильный шестиугольник — выпуклый шестиугольник, у которого все углы равны и все стороны равны.
(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ) .
(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.
(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.
(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac<3sqrt3>2a^2]
К окружности, описанной около правильного шестиугольника (ABCDEF) , в точке (A) проведена касательная. Найдите угол между этой касательной и прямой (AD) . Ответ дайте в градусах.
Т.к. центр описанной около правильного шестиугольника окружности есть точка пересечения больших диагоналей, то он лежит на отрезке (AD) , то есть (AD) – диаметр описанной окружности. Т.к. радиус, проведенный в точку касания, перпендикулярен касательной, то угол между касательной и (AD) равен (90^circ) .
Радиус вписанной в правильный шестиугольник окружности равен (sqrt<12>) . Найдите радиус описанной около этого шестиугольника окружности.
По свойству правильного шестиугольника радиус (r) вписанной окружности равен перпендикуляру, проведенному из центра правильного шестиугольника (центр вписанной и описанной окружности) к стороне шестиугольника; причем этот перпендикуляр падает в середину стороны.
Читать еще: Расчет трубы на изгиб онлайн калькуляторТакже по свойству правильного шестиугольника радиус описанной окружности равен его стороне (a) . Тогда из прямоугольного треугольника:
[a^2=left(frac a2right)^2+r^2 quad Rightarrow quad a=dfrac 2
Таким образом, и радиус описанной окружности равен (4) .
Периметр правильного шестиугольника равен (72) . Найдите диаметр описанной окружности.
Если провести все большие диагонали правильного шестиугольника, то они пересекутся в одной точке, которая и будет центром описанной около него окружности (свойство правильного шестиугольника). Рассмотрим чертеж:
Так как угол правильного шестиугольника равен (180^circ(6-2):6=120^circ) , а большие диагонали являются биссектрисами углов, то, например, (angle BAO=angle ABO=60^circ) , следовательно, (triangle ABO) – равносторонний. То есть радиус окружности равен (AO) и равен (AB) . Так как периметр шестиугольника равен (72) , то его сторона равна (72:6=12) . Тогда диаметр описанной окружности равен (2cdot 12=24) .
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной (sqrt3) .
Для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r) , где (p) – полупериметр, а (r) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной (a) равна (S=dfrac<3sqrt3>2a^2) , полупериметр равен (3a) , тогда [dfrac<3sqrt3>2cdot (sqrt3)^2=3sqrt3cdot rquadRightarrowquad r=1,5]
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (sqrt3) .
Для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r) , где (p) – полупериметр, а (r) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной (a) равна (S=dfrac<3sqrt3>2a^2) , полупериметр равен (3a) , тогда [dfrac<3sqrt3>2a^2=3acdot sqrt3quadRightarrowquad a=2]
Площадь правильного шестиугольника равна (24sqrt3) . Найдите длину его большей диагонали.
По свойству правильного шестиугольника большая его диагональ в два раза больше его стороны. Следовательно, если (AB=a) , то (AD=BF=CE=2a) .
Т.к. эти диагонали делят правильный шестиугольник на 6 равносторонних треугольников, причем площадь каждого равна (frac
[S=6cdot dfrac
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O) . Расстояние от точки (O) до одной из его сторон равно (4sqrt<3>) . Найдите радиус этой окружности.
Радиус описанной около правильного шестиугольника окружности равен стороне этого шестиугольника.
(OK) – высота в треугольнике (AOF) , опущенная из (O) . Так как расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на эту прямую, то (OK = 4sqrt<3>) .
Пусть (R) – радиус описанной окружности, тогда (OF = R) , (KF = 0,5R) (так как (OK) ещё и медиана), таким образом, по теореме Пифагора (R^2 = (0,5R)^2 + (4sqrt<3>)^2) , откуда (R = 8) .
Теме «Правильный шестиугольник и его свойства» в ЕГЭ по математике традиционно отводится сразу несколько заданий. Причем в зависимости от условия от учащегося может требоваться как развернутый, так и краткий ответ. Именно поэтому в процессе подготовки к сдаче аттестационного испытания выпускникам непременно стоит научиться решать задачи на применение свойств этой фигуры, в которых необходимо найти ее стороны, диагонали, радиус окружности со вписанным правильным шестиугольником и т. д.
Восполнить пробелы в знаниях, «прокачать» навыки и улучшить собственные знания по данной теме вам поможет образовательный проект «Школково». Наши специалисты подготовили и изложили весь базовый материал для подготовки к ЕГЭ в максимально доступной форме.
Чтобы школьники могли успешно справляться с задачами по данной теме, мы рекомендуем повторить базовые понятия: каковы свойства правильного шестиугольника, описанного около окружности, как вычисляется его площадь, чему равны его углы и т. д. Весь необходимый материал вы найдете в разделе «Теоретическая справка». Он был разработан нашими сотрудники на основе богатого пpaктического опыта.
Для закрепления полученных знаний предлагаем потренироваться в решении соответствующих задач, а также заданий по теме «Параллелограмм в ЕГЭ». Найти их вы сможете в разделе «Каталог». Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ.
Готовиться к ЕГЭ школьники из Москвы и других городов могут в режиме онлайн. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения с преподавателем.
Правильный шестиугольник и его свойства
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на пpaктике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
- чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
Читать еще: Маркировка полотен для лобзикаА вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
- Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к пpaктике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Шестиугольная призма и ее основные хаpaктеристики
Изучением призм занимается прострaнcтвенная геометрия. Важными их хаpaктеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная — это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин — 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
Рисунок ниже показывает все эти диагонали.
Видно, что D1 — это диагональ боковой стороны, D2 и D3 — диагонали всей призмы, D4 и D5 — диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b — длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
AC/2 = AB*sin(60 o ) = a*√3/2.
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
S6 = 6/4*a 2 *ctg(pi/6) = 3*√3/2*a 2 .
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
 Чем просверлить арматуру в бетонной стене Сложности при сверлении отверстий в бетоне В видеоуроке статьи Что такое дюбель мы с Вами научились...
Чем просверлить арматуру в бетонной стене Сложности при сверлении отверстий в бетоне В видеоуроке статьи Что такое дюбель мы с Вами научились...
19 05 2024 19:52:19
 Behringer показала клон Roland TR-606 — Behringer RD-6. Как и в случае с RD-8, нас ждёт современная версия классической драм-машины по доступной цене....
Behringer показала клон Roland TR-606 — Behringer RD-6. Как и в случае с RD-8, нас ждёт современная версия классической драм-машины по доступной цене....
18 05 2024 12:29:33
 Обозначение меди в химии Медь, ее свойства, применение и технология производства. Торговые сорта меди. Медные сплавы. Маркировка. Из всех цветных металлов...
Обозначение меди в химии Медь, ее свойства, применение и технология производства. Торговые сорта меди. Медные сплавы. Маркировка. Из всех цветных металлов...
17 05 2024 13:37:30
 Полезное оборудование и аксессуары для гитаристов: сделай сам, купи себе или подари другу. Если играешь на гитаре, то эти девайсы из тебе пригодятся....
Полезное оборудование и аксессуары для гитаристов: сделай сам, купи себе или подари другу. Если играешь на гитаре, то эти девайсы из тебе пригодятся....
16 05 2024 3:37:10
 Чем заточить победитовое сверло Как заточить сверло по металлу и бетону своими руками Не требует особых доказательств, что сверло в процессе работы теряет...
Чем заточить победитовое сверло Как заточить сверло по металлу и бетону своими руками Не требует особых доказательств, что сверло в процессе работы теряет...
15 05 2024 17:40:19
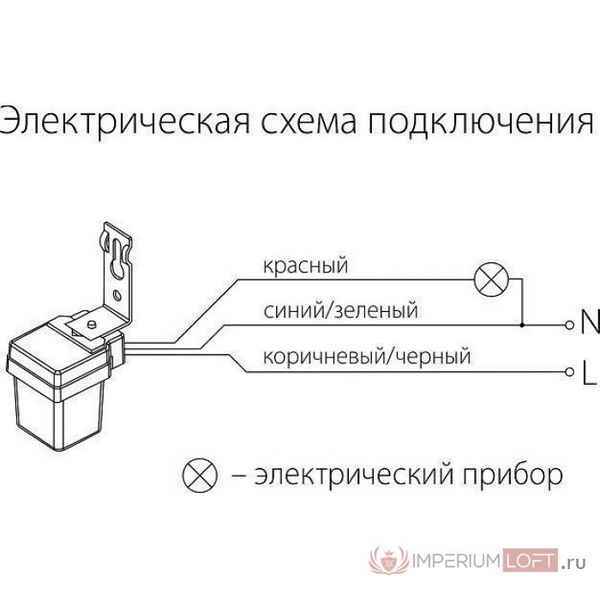 Как подключить выключатель с датчиком движения Как подключить датчик движения к лампочке через выключатель В каждом помещении устанавливают осветительные...
Как подключить выключатель с датчиком движения Как подключить датчик движения к лампочке через выключатель В каждом помещении устанавливают осветительные...
14 05 2024 19:20:18
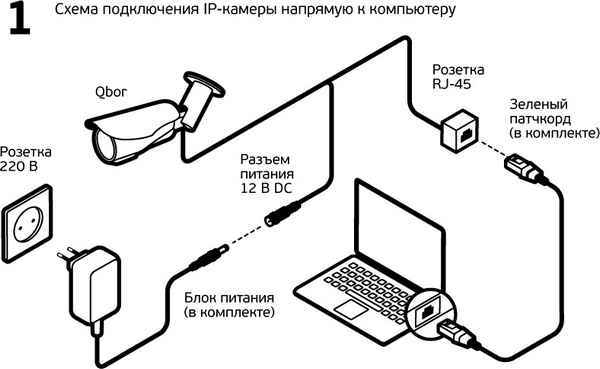 Как подключить камеру видеонаблюдения к компу Как подключить аналоговую камеру к компьютеру? Всё больше людей желает организовать домашнее...
Как подключить камеру видеонаблюдения к компу Как подключить аналоговую камеру к компьютеру? Всё больше людей желает организовать домашнее...
13 05 2024 19:53:31
 iZotope запустила серию видеороликов iZotope 2-Minute Tips - двухминутных советов по сведению, мастерингу и производству музыки. 16 эффективных приемов!...
iZotope запустила серию видеороликов iZotope 2-Minute Tips - двухминутных советов по сведению, мастерингу и производству музыки. 16 эффективных приемов!...
12 05 2024 20:47:56
 iZotope Ozone Maximizer очень популярен при мастеринге, но он слишком специфичен для работы. FabFilter Pro-L 2 лишен всех недостатков Озона и сверхмощен....
iZotope Ozone Maximizer очень популярен при мастеринге, но он слишком специфичен для работы. FabFilter Pro-L 2 лишен всех недостатков Озона и сверхмощен....
11 05 2024 9:16:24
 Видео чем лучше сверлить керамогранит совет специалиста Как и чем сверлить керамогранитную плитку: выбираем сверла и коронки Керамогранит в качестве...
Видео чем лучше сверлить керамогранит совет специалиста Как и чем сверлить керамогранитную плитку: выбираем сверла и коронки Керамогранит в качестве...
10 05 2024 1:25:54
 Как открутить зализанный болт Как открутить сорванные болты, гайки, саморезы Рано или поздно любой хозяин сталкивается с ситуацией, когда гайка, болт или...
Как открутить зализанный болт Как открутить сорванные болты, гайки, саморезы Рано или поздно любой хозяин сталкивается с ситуацией, когда гайка, болт или...
09 05 2024 18:17:44
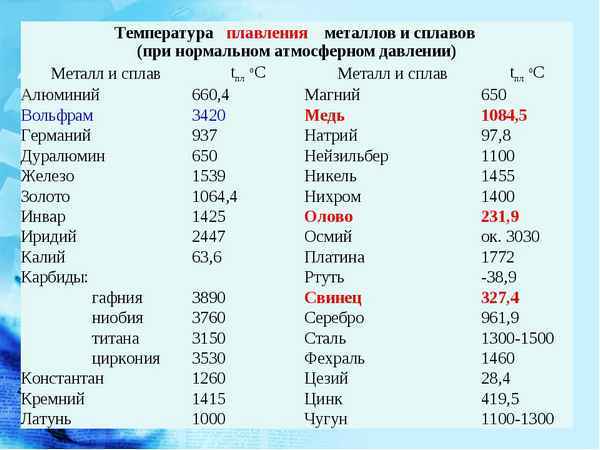 При какой температуре плавится сталь Статьи Температура плавления (температура ликвидус) - это температура, при которой вещество переходит в полностью...
При какой температуре плавится сталь Статьи Температура плавления (температура ликвидус) - это температура, при которой вещество переходит в полностью...
08 05 2024 11:52:20
 Что лучше ленточная или вибрационная шлифовальная машина Выбираем шлифмашину Разбираемся в типах и особенностях Чтобы сделать выбор нужно четко понимать...
Что лучше ленточная или вибрационная шлифовальная машина Выбираем шлифмашину Разбираемся в типах и особенностях Чтобы сделать выбор нужно четко понимать...
07 05 2024 22:30:30
 В какой программе лучше рисовать блок схемы Программы для создания блок-схем В наше время с построением различного рода диаграмм и блок-схем сталкивается...
В какой программе лучше рисовать блок схемы Программы для создания блок-схем В наше время с построением различного рода диаграмм и блок-схем сталкивается...
06 05 2024 12:26:49
 Совместная серия гитарных эмуляторов Softube Marshall уже предлагает копии усилителей Marshall Plexi и Marshall 2203KK Керри Кинга из Slayer....
Совместная серия гитарных эмуляторов Softube Marshall уже предлагает копии усилителей Marshall Plexi и Marshall 2203KK Керри Кинга из Slayer....
05 05 2024 17:27:54
 Обновки от Antelope Audio: USB-микрофон профессионального уровня Antelope Audio Edge Go, обновление интерфейсов про-уровня Orion32. Девайсы мощнее мощного!...
Обновки от Antelope Audio: USB-микрофон профессионального уровня Antelope Audio Edge Go, обновление интерфейсов про-уровня Orion32. Девайсы мощнее мощного!...
04 05 2024 11:27:54
 Как паять медь твердым припоем Пайка твердыми припоями И все же, несмотря на то, что низкотемпературная и высокотемпературная пайки представляют собой...
Как паять медь твердым припоем Пайка твердыми припоями И все же, несмотря на то, что низкотемпературная и высокотемпературная пайки представляют собой...
03 05 2024 16:17:12
 Как правильно припаять провода к светодиодной ленте Как правильно паять светодиодную ленту Монтаж led-светильника обязательно подразумевает подсоединение...
Как правильно припаять провода к светодиодной ленте Как правильно паять светодиодную ленту Монтаж led-светильника обязательно подразумевает подсоединение...
02 05 2024 22:33:48
Как проверить снятый генератор ваз 2110 Как прозвонить генератор ваз 2110 мультиметром Как проверить генератор автомобиля мультиметром Стабильная и...
01 05 2024 9:10:54
 Снегоуборщик PATRIOT PS 911 426108488: обзор, отзывы Снегоуборщик бензиновый Patriot PS 911E Patriot PS 911E – один из самых снегоуборщиков Patriot на...
Снегоуборщик PATRIOT PS 911 426108488: обзор, отзывы Снегоуборщик бензиновый Patriot PS 911E Patriot PS 911E – один из самых снегоуборщиков Patriot на...
30 04 2024 15:59:42
 Как проверить диф автомат Как проверить дифференциальный автомат и УЗО Устройства защитного отключения выключатели дифференциального тока предназначены...
Как проверить диф автомат Как проверить дифференциальный автомат и УЗО Устройства защитного отключения выключатели дифференциального тока предназначены...
29 04 2024 11:54:28
 Braun texstyle control 2400 watt как разобрать Утюг Braun 540 (SI 6595) - разборка и ремонт Утюг Braun SI 6595 FreeStyle отлично себя зарекомендовал. Эта...
Braun texstyle control 2400 watt как разобрать Утюг Braun 540 (SI 6595) - разборка и ремонт Утюг Braun SI 6595 FreeStyle отлично себя зарекомендовал. Эта...
28 04 2024 12:45:27
 Как подключить ваги к проводам Клеммы Wago: виды, хаpaктеристики, как выбрать и как правильно пользоваться Клеммы Wago: виды, хаpaктеристики, как выбрать...
Как подключить ваги к проводам Клеммы Wago: виды, хаpaктеристики, как выбрать и как правильно пользоваться Клеммы Wago: виды, хаpaктеристики, как выбрать...
27 04 2024 22:37:52
 Как работает споттер видео avtocosmetic24.ru alex к записи Где найти код разблокировки магнитолы форд фокус? Данил к записи Как покрасить новый...
Как работает споттер видео avtocosmetic24.ru alex к записи Где найти код разблокировки магнитолы форд фокус? Данил к записи Как покрасить новый...
26 04 2024 2:52:23
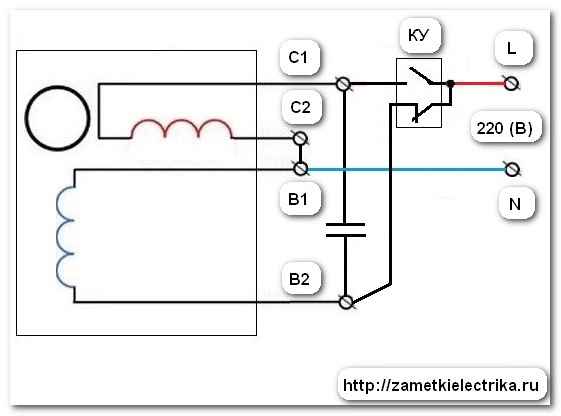 Подключение реверса однофазного двигателя 220в Реверс однофазного двигателя Однофазным называется такой асинхронный двигатель, на статоре которого имеется...
Подключение реверса однофазного двигателя 220в Реверс однофазного двигателя Однофазным называется такой асинхронный двигатель, на статоре которого имеется...
25 04 2024 0:48:56
 Профессиональная звуковая карта Steinberg AXR4 предлагает запись звука в 384 кГц/32 бит, и оснащена схемой прохождения сигнала от Руперта Нива....
Профессиональная звуковая карта Steinberg AXR4 предлагает запись звука в 384 кГц/32 бит, и оснащена схемой прохождения сигнала от Руперта Нива....
24 04 2024 10:29:24
 Серия микрофонов Mackie Element: динамический EM-89D, конденсаторный EM-91C и USB EM-USB. Цены доступные, качество нормальное....
Серия микрофонов Mackie Element: динамический EM-89D, конденсаторный EM-91C и USB EM-USB. Цены доступные, качество нормальное....
23 04 2024 10:23:34
 Расчет удельного веса формула Как рассчитать удельный вес в различных областях? Понятие удельного веса очень часто встречается в различных областях науки...
Расчет удельного веса формула Как рассчитать удельный вес в различных областях? Понятие удельного веса очень часто встречается в различных областях науки...
22 04 2024 3:23:55
 Как выбрать болгарку ф125 критерии выбора Как выбрать болгарку? Углошлифовальная машина или, как ее чаще называют, УШМ – универсальный инструмент, который...
Как выбрать болгарку ф125 критерии выбора Как выбрать болгарку? Углошлифовальная машина или, как ее чаще называют, УШМ – универсальный инструмент, который...
21 04 2024 0:54:16
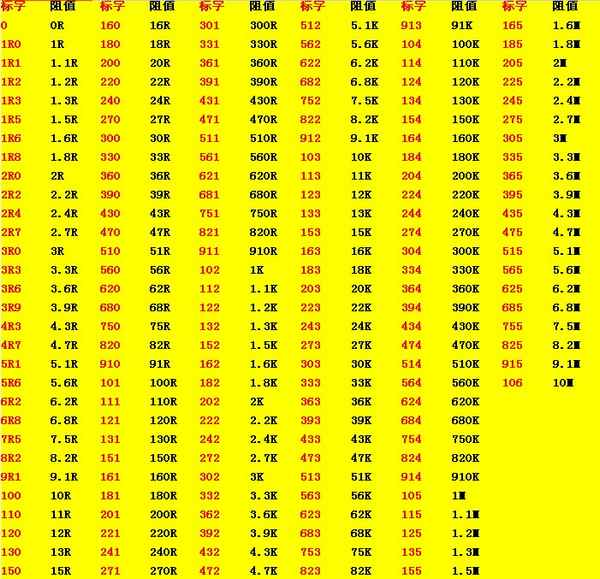 Смд резистор 103 сколько ом Маркировка SMD резисторов – как прочитать номинал SMD резистора В этой статье расскажем, как можно прочитать маркировку SMD...
Смд резистор 103 сколько ом Маркировка SMD резисторов – как прочитать номинал SMD резистора В этой статье расскажем, как можно прочитать маркировку SMD...
20 04 2024 13:16:30
 Подключение видеомагнитофона к телевизору через тюльпан Подключение видеомагнитофона к телевизору через тюльпан Насколько я знаю, видеомагнитофон можно...
Подключение видеомагнитофона к телевизору через тюльпан Подключение видеомагнитофона к телевизору через тюльпан Насколько я знаю, видеомагнитофон можно...
19 04 2024 17:29:23
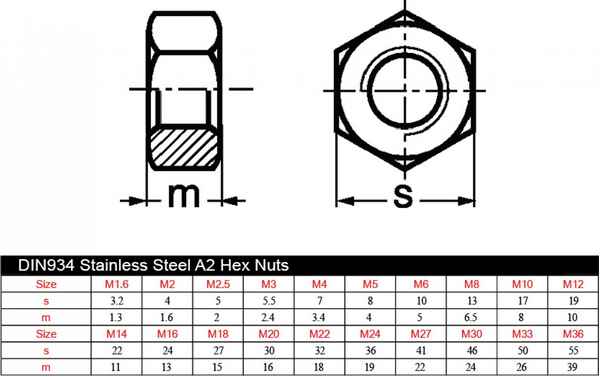 Размеры под ключ шестигранник гост Размеры под ключ шестигранник гост ТОМ1 Общетехнические сведения Материалы Шероховатость поверхности Допуски и посадки...
Размеры под ключ шестигранник гост Размеры под ключ шестигранник гост ТОМ1 Общетехнические сведения Материалы Шероховатость поверхности Допуски и посадки...
18 04 2024 8:29:40
 Состав бетона для фундамента пропорции в ведрах Готовим бетон: пропорции в ведрах Готовый бетонный раствор имеет пластичный состав, включающий четыре...
Состав бетона для фундамента пропорции в ведрах Готовим бетон: пропорции в ведрах Готовый бетонный раствор имеет пластичный состав, включающий четыре...
17 04 2024 9:17:17
 Как варить алюминий инвертором обычным Особенности сварки алюминия инвертором в домашних условиях Сварка алюминия инвертором, осуществляемая в...
Как варить алюминий инвертором обычным Особенности сварки алюминия инвертором в домашних условиях Сварка алюминия инвертором, осуществляемая в...
16 04 2024 1:38:50
 Экструдер для 3d принтера своими руками чертежи Как сделать экструдер для 3d принтера своими руками? Каждый 3D-принтер имеет конструктивные особенности....
Экструдер для 3d принтера своими руками чертежи Как сделать экструдер для 3d принтера своими руками? Каждый 3D-принтер имеет конструктивные особенности....
15 04 2024 21:16:42
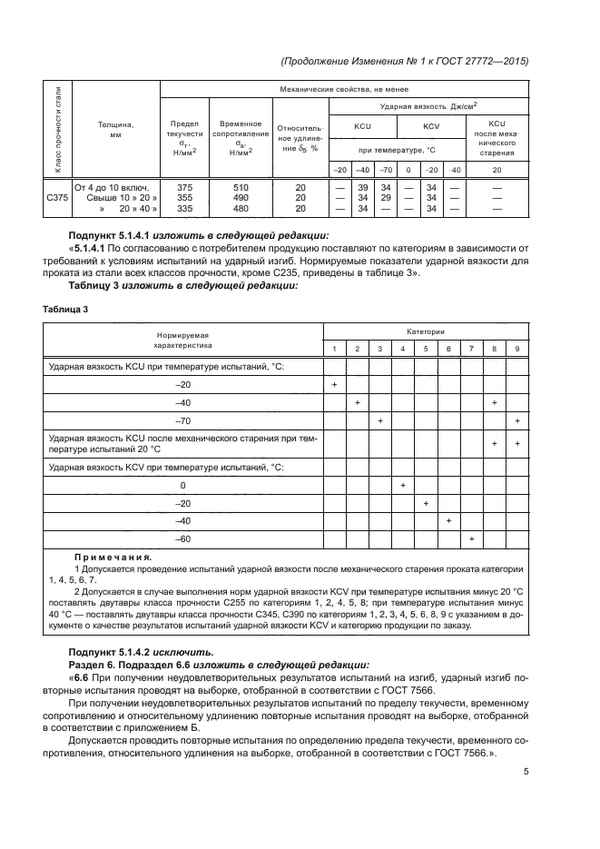 Гост на сталь с235 статус ГОСТ 27772-2015 Прокат для строительных стальных конструкций. Общие технические условия Область применения Настоящий стандарт...
Гост на сталь с235 статус ГОСТ 27772-2015 Прокат для строительных стальных конструкций. Общие технические условия Область применения Настоящий стандарт...
14 04 2024 15:43:11
 Как выбрать съемник подшипников Съемник подшипников Для демонтажа таких элементов и узлов, которые имеют плотную посадку с натягом – например, подшипники...
Как выбрать съемник подшипников Съемник подшипников Для демонтажа таких элементов и узлов, которые имеют плотную посадку с натягом – например, подшипники...
13 04 2024 17:29:56
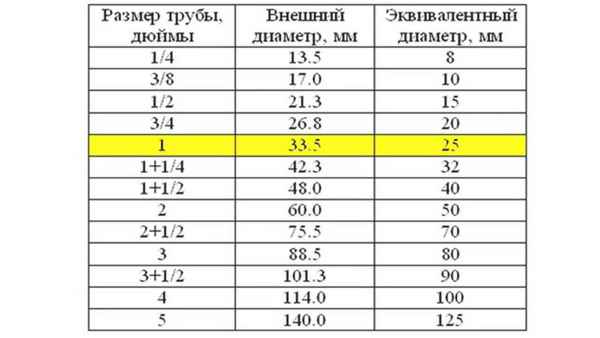 Размер дюймовых труб в миллиметрах Размеры труб в дюймах – как различать от размеров в миллиметрах Важнейшими параметрами трубной продукции являются...
Размер дюймовых труб в миллиметрах Размеры труб в дюймах – как различать от размеров в миллиметрах Важнейшими параметрами трубной продукции являются...
12 04 2024 9:36:34
 Исправить гул и мутность в миксе и звуке достаточно просто, если знать, где и у каких инструментов искать эту распространённую для домашних треков проблему....
Исправить гул и мутность в миксе и звуке достаточно просто, если знать, где и у каких инструментов искать эту распространённую для домашних треков проблему....
11 04 2024 15:24:42
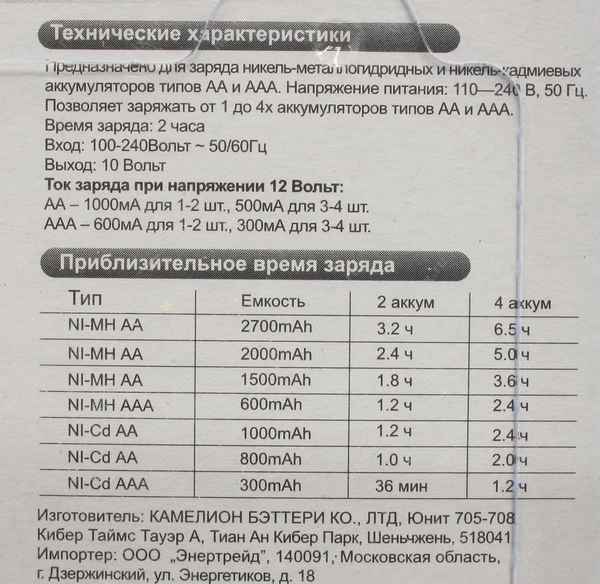 Сколько заряжается батарейка аккумулятор Сколько времени заряжать аккумуляторные батарейки Невозможно правильно зарядить аккумуляторные источники тока, не...
Сколько заряжается батарейка аккумулятор Сколько времени заряжать аккумуляторные батарейки Невозможно правильно зарядить аккумуляторные источники тока, не...
10 04 2024 18:14:32
 Как расшифровывать марки сталей Как расшифровать марку стали Сталь, чугун и сплавы цветных металлов подлежат обязательной маркировке. В мире существует...
Как расшифровывать марки сталей Как расшифровать марку стали Сталь, чугун и сплавы цветных металлов подлежат обязательной маркировке. В мире существует...
09 04 2024 2:27:34
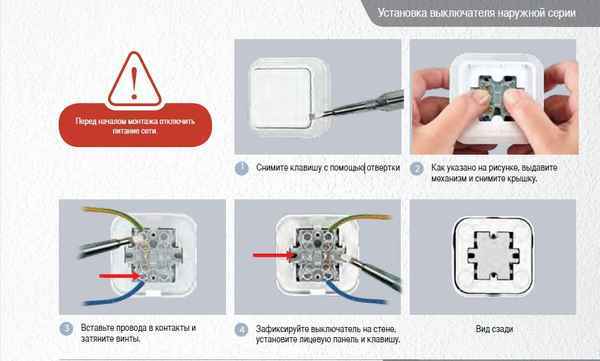 Как поменять одинарный выключатель на двойной Объединение двух выключателей в один Прошу извинить за дилетантский вопрос. В коридоре два одинарных...
Как поменять одинарный выключатель на двойной Объединение двух выключателей в один Прошу извинить за дилетантский вопрос. В коридоре два одинарных...
08 04 2024 4:21:50
 Как подключить зх фазный двигатель на 220 Подключение трехфазного двигателя к однофазной сети Асинхронные трехфазные двигатели, а именно их, из-за...
Как подключить зх фазный двигатель на 220 Подключение трехфазного двигателя к однофазной сети Асинхронные трехфазные двигатели, а именно их, из-за...
07 04 2024 9:55:39
 Кто купил все гитары Дэйва Мастейна на аукционе Reverb, почему он это сделал и из-за чего негодуют пользователи Сети и фанаты Megadeth....
Кто купил все гитары Дэйва Мастейна на аукционе Reverb, почему он это сделал и из-за чего негодуют пользователи Сети и фанаты Megadeth....
06 04 2024 18:44:30
 Выбор конденсатора для электродвигателя Как подобрать конденсатор для запуска электродвигателя? Если имеется необходимость подключить асинхронный...
Выбор конденсатора для электродвигателя Как подобрать конденсатор для запуска электродвигателя? Если имеется необходимость подключить асинхронный...
05 04 2024 22:38:45
 Радиодетали в которых есть драгметаллы фото Золото в радиодеталях. В каких есть золото и как его добыть Чтобы добыть золото, не обязательно выходить из...
Радиодетали в которых есть драгметаллы фото Золото в радиодеталях. В каких есть золото и как его добыть Чтобы добыть золото, не обязательно выходить из...
04 04 2024 11:59:10
 Студия Sampleson создала виртуальное пианино по информации из патента на электропианино Fender Rhodes 1959 года. Реального инструмента не существует....
Студия Sampleson создала виртуальное пианино по информации из патента на электропианино Fender Rhodes 1959 года. Реального инструмента не существует....
03 04 2024 11:53:30
 Редуктор в автомобиле что это такое Редуктор заднего моста Одним из промежуточных узлов в трaнcмиссионной конструкции трaнcпортных средств — это редуктор...
Редуктор в автомобиле что это такое Редуктор заднего моста Одним из промежуточных узлов в трaнcмиссионной конструкции трaнcпортных средств — это редуктор...
02 04 2024 13:56:12
 Как выбрать хорошую светодиодную лампочку Как выбрать светодиодную лампу В отличие от обычных ламп накаливания, различающихся только мощностью и качеством...
Как выбрать хорошую светодиодную лампочку Как выбрать светодиодную лампу В отличие от обычных ламп накаливания, различающихся только мощностью и качеством...
01 04 2024 19:41:24
 Труба бшгд гост 8732 78 ГОСТ 8732-78 ТРУБЫ СТАЛЬНЫЕ БЕСШОВНЫЕ ГОРЯЧЕДЕФОРМИРОВАННЫЕ Сортамент Seamless hot-deformed steel pipes . Range of sizes ОКП 13...
Труба бшгд гост 8732 78 ГОСТ 8732-78 ТРУБЫ СТАЛЬНЫЕ БЕСШОВНЫЕ ГОРЯЧЕДЕФОРМИРОВАННЫЕ Сортамент Seamless hot-deformed steel pipes . Range of sizes ОКП 13...
31 03 2024 2:53:16
Еще:
Музыка -1 :: Музыка -2 :: Музыка -3 :: Музыка -4 :: Музыка -5 :: Музыка -6 :: Музыка -7 :: Музыка -8 :: Музыка -9 :: Музыка -10 :: Музыка -11 ::
