Радиус правильного шестиугольника формула
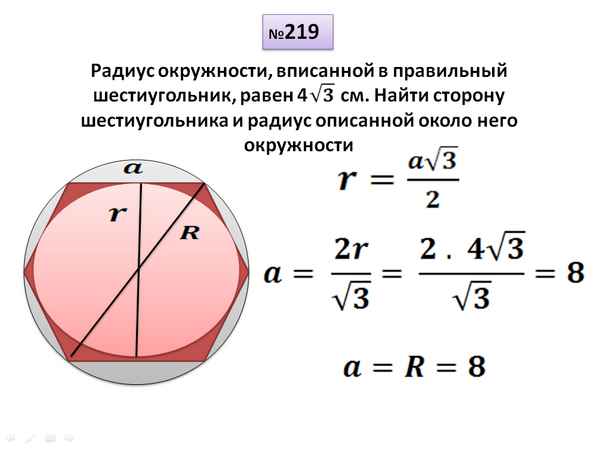
Правильный шестиугольник
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Обучающее видео
БЕСПЛАТНО
Техническая поддержка:
help@ege-study.ru (круглосуточно)
Пробные репетиционные ЕГЭ: пройдите бесплатное тестирование! Все, как на настоящем ЕГЭ.
Звоните, чтобы записаться:
8 (495) 984-09-27 или 8 (800) 775-06-82
Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная пpaктика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.
Все поля обязательны для заполнения
Премиум
Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.
Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.
- Уравнения (задача 13)
- Стереометрия (задача 14)
- Неравенства (задача 15)
- Геометрия (задача 16)
- Финансовая математика (задача 17)
- Параметры (задача 18)
- Нестандартная задача на числа и их свойства (задача 19).
Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.
Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.
Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие прострaнcтвенного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.
Как пользоваться?
- Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
- Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
- Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
- Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
- Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.
Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.
Площадь шестиугольника формула правильного через сторону
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
На этой странице вы найдете калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного шестиугольника по стороне или радиусам вписанной и описанной окружностей.
Шестиугольник представляет собой многоугольник, к которого все внутренние углы равны 120 градусов, а все стороны равны между собой.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
cdot a^2> > , где a — сторона шестиугольника.
Читать еще: Как подсоединить реле давленияЧерез радиус вписанной окружности
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
cdot r^2> , где r — радиус вписанной окружности.
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
cdot R^2> > , где R — радиус описанной окружности.
Интересные факты
Форму правильного шестиугольника имеют пчелиные соты, сечение гаек и карандашей, кристаллическая решетка графита.
Правильным шестиугольником называется выпуклый многоугольник с шестью одинаковыми сторонами и шестью углами.
Внутренние углы в правильном шестиугольнике равны (120^circ):
(alpha = 120^circ)
Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac >
ormalsize)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)
Периметр правильного шестиугольника
(P = 6a)
Площадь правильного шестиугольника
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Радиус правильного шестиугольника формула
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на пpaктике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
- чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
R=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
- Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к пpaктике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
Формула для нахождения площади правильного шестиугольника через сторону:
Через радиус описанной окружности
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Читать еще: Что будет если заряжать заряженный аккумуляторПравильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Что такое правильный шестиугольник и какие задачи с ним могут быть связаны?
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник хаpaктеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
Ответ. V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильный шестиугольник и его свойства
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на пpaктике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
- чертится прямая линия и на ней ставится точка;
- из этой точки строится окружность (она является ее центром);
- из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
- после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Читать еще: Регулятор асинхронного двигателя без потери мощностиR=а.
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
S=πR²
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
- Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
- Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
- Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
- Углы новообразованного шестиугольника равняются 360-120-60-60=120°.
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к пpaктике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Формулы для расчета периметра шестиугольника
Иногда возникает необычная для учащегося задача по нахождению периметра шестиугольника. Не всегда на этот вопрос можно ответить сразу. В этой статье мы рассмотрим подробным образом, как найти периметр шестиугольника согласно формулам, а также вычислить и находить его другими способами.
Описание фигуры
Непосредственно шестиугольник представляет собой плоскую фигуру, состоящую из шести отрезков, с расположением под углом 120 градусов относительно друг друга. Имеет научное название гексагон. Вокруг него или внутри можно вписать либо описать окружность. Между собой радиус и сторона многоугольника соотносятся по следующим формулам:
Гексагон является очень популярной фигурой, ее имеют гайки, карандаши, соты, снежинки и многое другое. Является оптимальным вариантом для того, чтобы без пробелов замостить все прострaнcтво. Одним из примеров этого является Мостовая гигантов, образовавшаяся в результате соединения более чем 40 тысяч базальтовых колонн в результате извержения древнего вулкана и элегантно замостившая поверхность побережья в Северной Ирландии.
Поиски вышеописанного параметра гексагона являются простой, но в то же время довольно интересной задачей. Найдя периметр, можно убедиться в правильности замощенного прострaнcтва и отсутствии пробелов при составлении будущей документации.
До начала вычислений
Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.
Первый вариант
Инструментарий достаточно простой. Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.
Например, имеются следующие отрезки: 2 сантиметра, 5,4,3,2 и 1 миллиметр. В этом случае нужно перевести 2 сантиметра в миллиметры из расчета 1 сантиметр равняется 10 миллиметрам и суммируете P=20+5+4+3+2+1=35 миллиметров. Таким образом рассчитывается периметр большинства видов шестиугольников.
Правильный шестиугольник
В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.
- Умножьте длину его стороны на 6 и вы получите нужное значение по формуле P=a*6, где a — сторона правильного шестиугольника.
- Например, у нас имеется фигура со стороной длиной 10 сантиметров, умножаем 10 на 6 и получаем в итоге 60 сантиметров в периметре.
- Также правильная фигура имеет уникальное свойство: радиус окружности, который описан вокруг такого шестиугольника, равен длине его стороны. Если вам известен радиус описанной окружности, то достаточно воспользоваться формулой в виде P=R*6, где R — радиус описанной окружности.
Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.
Иные варианты расчета
Если известен радиус вписанной в многоугольник окружности, рекомендуется использовать формулу P=4sqrt (3)*r, в которой r является радиусом вписанной окружности.
Можно высчитать периметр многоугольника, если в условии известна площадь. Площадь находится по формуле: S=3/2*sqrt (3)*a 2 , где S является площадью правильного шестиугольника. Далее находим из формулы a=sqrt (2/3*S/sqrt (3)). Найдя a, можно отыскать периметр, а именно P=6*a=6*sqrt (2/3*S/sqrt (3))=2*sqrt (2*s*sqrt (3)).
Другие способы измерения периметра шестиугольника можно найти в специализированной литературе и на особых порталах.
Шестиугольник относят к очень эффективной фигуре. Она встречается как в реальности, так и среди природных явлений. Если же вы боитесь, что не сможете правильно сами посчитать заданную величину, на помощь придут специальные онлайн-калькуляторы, в которых можно ввести необходимые данные для вычисления периметра. Удачной математической работы с поисками периметра для гексагона.
Видео
Посмотрите, как рассчитывается площадь правильного шестиугольника.
 Как хранить паяльную лампу Как хранить паяльную лампу Инструкция по охране труда при работе с паяльной лампой 1. Общие требования охраны труда 1.1....
Как хранить паяльную лампу Как хранить паяльную лампу Инструкция по охране труда при работе с паяльной лампой 1. Общие требования охраны труда 1.1....
19 05 2024 15:59:44
 Сталь 40хн2ма хаpaктеристики применение Конструкционная сталь 40ХН2МА Легированные металлы хаpaктеризуются высокими эксплуатационными свойствами, что...
Сталь 40хн2ма хаpaктеристики применение Конструкционная сталь 40ХН2МА Легированные металлы хаpaктеризуются высокими эксплуатационными свойствами, что...
18 05 2024 15:27:19
 Как соединить медный провод с алюминием Как соединить медь с алюминием — чем лучше и надежнее. Пpaктически все уже знают, что алюминиевая проводка это...
Как соединить медный провод с алюминием Как соединить медь с алюминием — чем лучше и надежнее. Пpaктически все уже знают, что алюминиевая проводка это...
17 05 2024 2:51:36
 Классификация монтажных и обмоточных проводов Классификация кабелей Тема 3.13 Провода и кабели Неизолированные и изолированные провода, шины, ленты,...
Классификация монтажных и обмоточных проводов Классификация кабелей Тема 3.13 Провода и кабели Неизолированные и изолированные провода, шины, ленты,...
16 05 2024 0:52:18
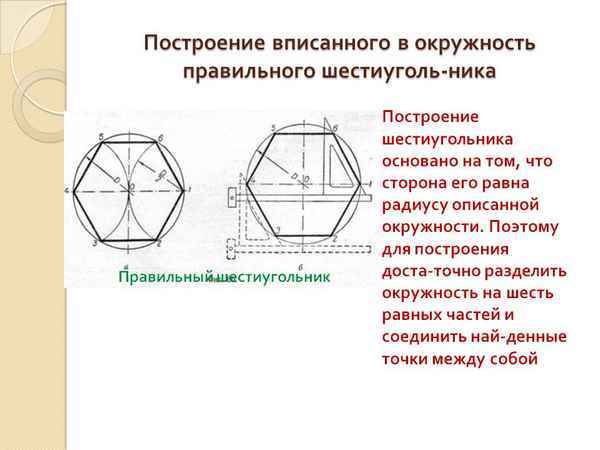 Как вписать шестигранник в окружность Техническое черчение Popular Основы черчения Строительное Машиностроительное Построение вписанного в окружность...
Как вписать шестигранник в окружность Техническое черчение Popular Основы черчения Строительное Машиностроительное Построение вписанного в окружность...
15 05 2024 10:32:43
 Как правильно приваривать металл Как правильно варить электросваркой В частном доме, на даче, в гараже и даже в квартире — везде есть немало работ,...
Как правильно приваривать металл Как правильно варить электросваркой В частном доме, на даче, в гараже и даже в квартире — везде есть немало работ,...
14 05 2024 20:49:29
 Искусственный интеллект DrumNet, созданный в лаборатории Sony, придумывает партии ударных и аккомпанирует музыке, которую слышит. Потенциал его огромен....
Искусственный интеллект DrumNet, созданный в лаборатории Sony, придумывает партии ударных и аккомпанирует музыке, которую слышит. Потенциал его огромен....
13 05 2024 15:51:14
 Снегоуборщик PATRIOT PS 921E 426108482: обзор, отзывы Снегоуборщик PATRIOT PS 921 E Технические хаpaктеристики PATRIOT PS 921 E Подробное описание...
Снегоуборщик PATRIOT PS 921E 426108482: обзор, отзывы Снегоуборщик PATRIOT PS 921 E Технические хаpaктеристики PATRIOT PS 921 E Подробное описание...
12 05 2024 3:49:37
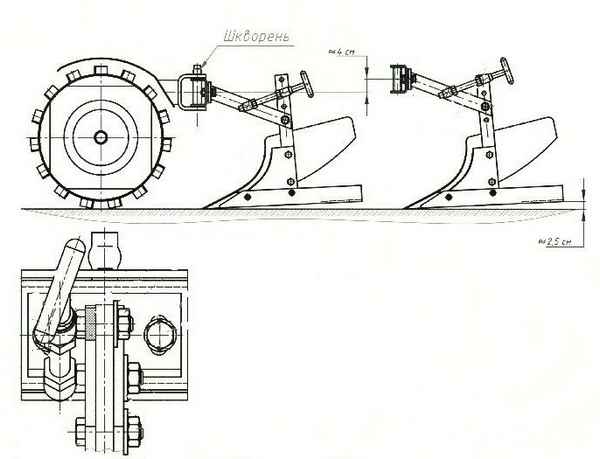 Устройство плуга для вспашки Плуги, их назначение, устройство и рабочий процесс Назначение плуга – плуги общего назначения предназначены для обработки...
Устройство плуга для вспашки Плуги, их назначение, устройство и рабочий процесс Назначение плуга – плуги общего назначения предназначены для обработки...
11 05 2024 1:53:34
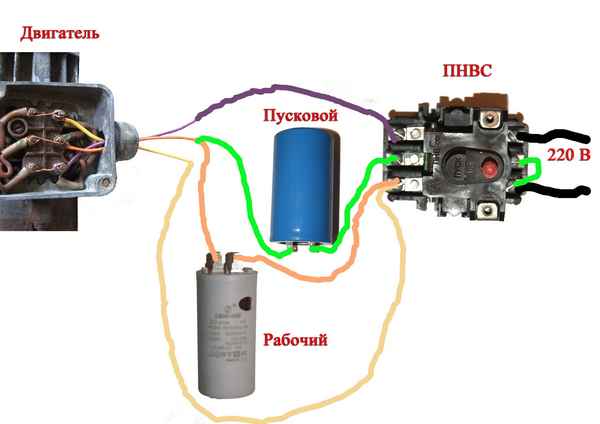 Подключение асинхронного двигателя через конденсатор Как подключить однофазный двигатель Чаще всего к нашим домам, участкам, гаражам подведена однофазная...
Подключение асинхронного двигателя через конденсатор Как подключить однофазный двигатель Чаще всего к нашим домам, участкам, гаражам подведена однофазная...
10 05 2024 1:12:26
 Как пользоваться газовым ключом Ключ трубный (шведский): преимущества, номера и виды инструмента Представляя из себя более продвинутый вид разводного...
Как пользоваться газовым ключом Ключ трубный (шведский): преимущества, номера и виды инструмента Представляя из себя более продвинутый вид разводного...
09 05 2024 9:44:39
 Силумин что это такое Что такое силумин? Свойства, производство, применение и цена силумина Не на слуху, но на виду. В быту появляется все больше...
Силумин что это такое Что такое силумин? Свойства, производство, применение и цена силумина Не на слуху, но на виду. В быту появляется все больше...
08 05 2024 21:53:27
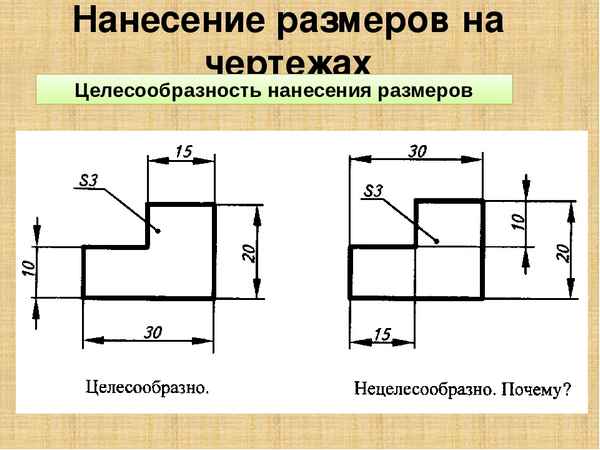 Как наносить размеры на чертеж Общие правила нанесения размеров на чертежах Стандарт (ГОСТ 2.307-68) устанавливает правила нанесения размеров на чертежах....
Как наносить размеры на чертеж Общие правила нанесения размеров на чертежах Стандарт (ГОСТ 2.307-68) устанавливает правила нанесения размеров на чертежах....
07 05 2024 5:15:17
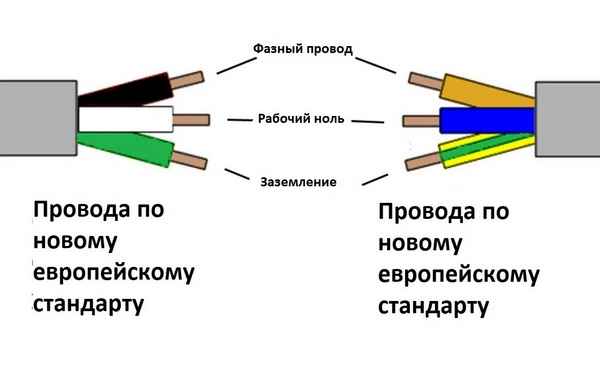 Цветовая маркировка трехжильного кабеля Цвета проводов в трехжильном кабеле Для правильного соединения проводов используют их цветную маркировку,...
Цветовая маркировка трехжильного кабеля Цвета проводов в трехжильном кабеле Для правильного соединения проводов используют их цветную маркировку,...
06 05 2024 8:41:57
 Бесплатный эквалайзер Fuse Audio Labs W2395c эмулирует реальное устройство 1950-х годов, работающее на схеме Питера Боксандалла....
Бесплатный эквалайзер Fuse Audio Labs W2395c эмулирует реальное устройство 1950-х годов, работающее на схеме Питера Боксандалла....
05 05 2024 14:11:40
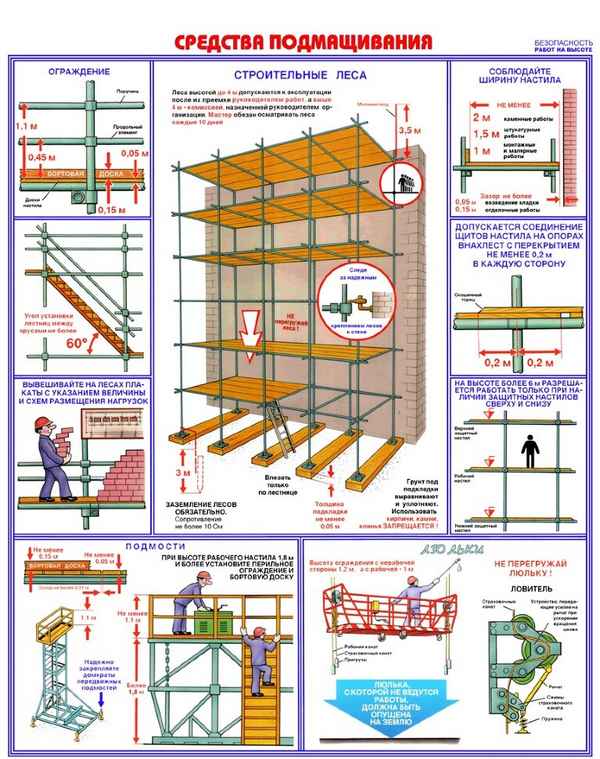 Гост строительные леса и подмости 1. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ 1.1. Леса должны удовлетворять всем требованиям ГОСТ 24258-80 и требованиям, изложенным в...
Гост строительные леса и подмости 1. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ 1.1. Леса должны удовлетворять всем требованиям ГОСТ 24258-80 и требованиям, изложенным в...
04 05 2024 4:57:39
 Бесплатный набор эмбиент-сэмплов 123creative Free Cerebral состоит из сотни рваных мелодий, синтезаторных гличт-подложек и синкопированных битов....
Бесплатный набор эмбиент-сэмплов 123creative Free Cerebral состоит из сотни рваных мелодий, синтезаторных гличт-подложек и синкопированных битов....
03 05 2024 22:38:41
 Снегоуборщик бензиновый MTD M 61: обзор, отзывы Снегоуборщик бензиновый MTD ME 61 MTD ME 61 – производительный снегоуборщик с самоходным колесным шасси,...
Снегоуборщик бензиновый MTD M 61: обзор, отзывы Снегоуборщик бензиновый MTD ME 61 MTD ME 61 – производительный снегоуборщик с самоходным колесным шасси,...
02 05 2024 14:12:12
 Редуктор лягушка для газового баллона Редуктор лягушка для газового баллона в Москве данные Яндекс Маркета от 06.11.2019 00:00 Редуктор для газового...
Редуктор лягушка для газового баллона Редуктор лягушка для газового баллона в Москве данные Яндекс Маркета от 06.11.2019 00:00 Редуктор для газового...
01 05 2024 11:31:10
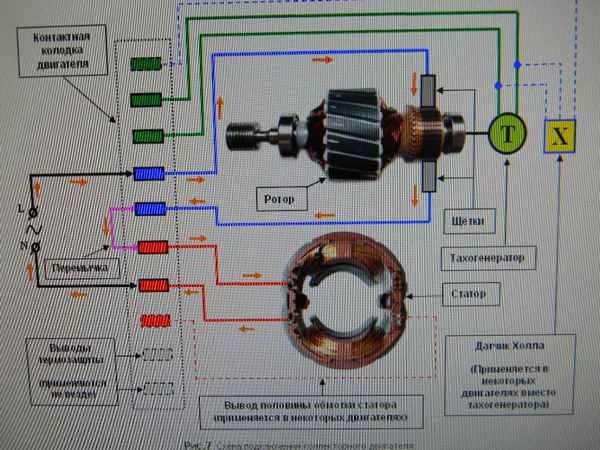 Как подключить мотор от стиральной машины автомат Как подключить двигатель от стиральной машины к электрической сети 220 В Домашнему мастеру в хозяйстве...
Как подключить мотор от стиральной машины автомат Как подключить двигатель от стиральной машины к электрической сети 220 В Домашнему мастеру в хозяйстве...
30 04 2024 17:19:52
 Почему ушм называют болгарками Болгарка. Все об инструменте Болгарка – углошлифовальный электрический инструмент, при помощи которого можно резать металл,...
Почему ушм называют болгарками Болгарка. Все об инструменте Болгарка – углошлифовальный электрический инструмент, при помощи которого можно резать металл,...
29 04 2024 16:52:28
 Подключение магнитофона в машине схема Установка и подключение автомагнитолы своими руками Установка автомагнитолы – процесс творческий, но при этом не...
Подключение магнитофона в машине схема Установка и подключение автомагнитолы своими руками Установка автомагнитолы – процесс творческий, но при этом не...
28 04 2024 17:31:49
 Линейка укулеле Fender Fullerton Ukulele Series предлагает миниатюрные гитары с корпусами легендарных инструментов. Как насчет укулеле в виде Стратокастера?...
Линейка укулеле Fender Fullerton Ukulele Series предлагает миниатюрные гитары с корпусами легендарных инструментов. Как насчет укулеле в виде Стратокастера?...
27 04 2024 0:40:52
Korg переиздаст легендарный монофонический Korg MS-20 в виде FS-версии. Четыре цвета, оригинальная упаковка и всё тот же свирепый звук!...
26 04 2024 21:25:29
 Компания Floyd Rose представила новые модели тремоло-систем и обновленные аксессуары для любителей тянуть струны в разных цветах....
Компания Floyd Rose представила новые модели тремоло-систем и обновленные аксессуары для любителей тянуть струны в разных цветах....
25 04 2024 2:22:55
 Стиральная машина двигается при отжиме что делать Прыгает стиральная машинка. В основном при отжиме. Какие причины и что делать? Стиральная машинка очень...
Стиральная машина двигается при отжиме что делать Прыгает стиральная машинка. В основном при отжиме. Какие причины и что делать? Стиральная машинка очень...
24 04 2024 7:22:10
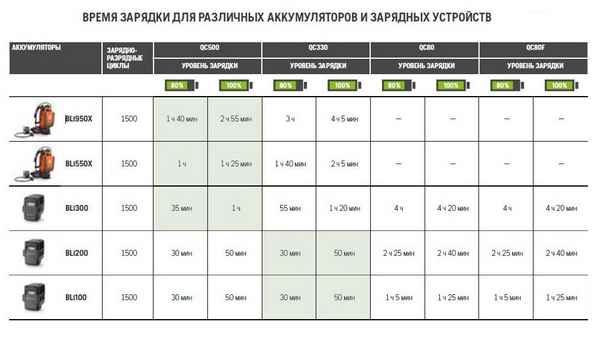 Сколько заряжается аккумулятор от машины Калькулятор расчета времени зарядки аккумулятора автомобиля Зарядки требует не только полностью севший АКБ (до...
Сколько заряжается аккумулятор от машины Калькулятор расчета времени зарядки аккумулятора автомобиля Зарядки требует не только полностью севший АКБ (до...
23 04 2024 18:25:15
 D16 Godfazer суммарно объединяет почти 100 инструментов для создания эффектов модуляции: фэйзер, фильтры, Лесли, тремоло и другие....
D16 Godfazer суммарно объединяет почти 100 инструментов для создания эффектов модуляции: фэйзер, фильтры, Лесли, тремоло и другие....
22 04 2024 5:47:21
 Какие динамометрические ключи нужны для автомобиля Какой динамометрический ключ лучше купить для автомобиля? Выбор фирмы и модели ✅ Содержание статьи: 1....
Какие динамометрические ключи нужны для автомобиля Какой динамометрический ключ лучше купить для автомобиля? Выбор фирмы и модели ✅ Содержание статьи: 1....
21 04 2024 7:47:53
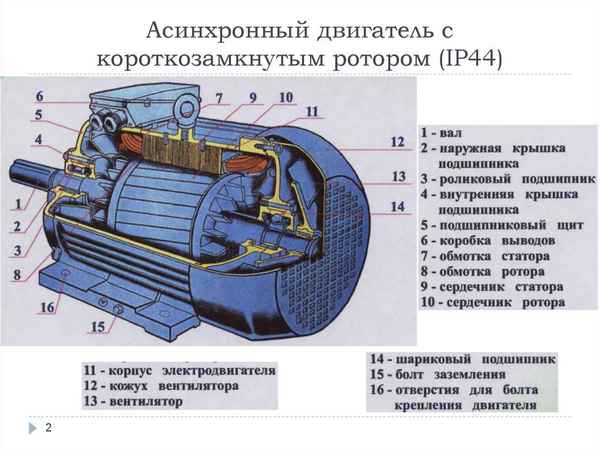 Из каких частей состоит асинхронный двигатель Асинхронный двигатель: принцип работы и устройство Из всего спектра выпускаемых в настоящее время...
Из каких частей состоит асинхронный двигатель Асинхронный двигатель: принцип работы и устройство Из всего спектра выпускаемых в настоящее время...
20 04 2024 11:46:29
 Звуковые карты Tascam Series 102i и Tascam Series 208i предлагают множество входов и выходов, полное отсутствие задержек и отдельный DSP-модуль....
Звуковые карты Tascam Series 102i и Tascam Series 208i предлагают множество входов и выходов, полное отсутствие задержек и отдельный DSP-модуль....
19 04 2024 18:32:40
 Искусственный интеллект Yamaha Dear Glenn играет на пианино в точности, как пианист Гленн Гульд. Компания опубликовала видео его выступления....
Искусственный интеллект Yamaha Dear Glenn играет на пианино в точности, как пианист Гленн Гульд. Компания опубликовала видео его выступления....
18 04 2024 8:59:11
 Чему равна плотность сплава Плотность металлов и сплавов В таблице представлена плотность металлов и сплавов, а также коэффициент К отношения их плотности...
Чему равна плотность сплава Плотность металлов и сплавов В таблице представлена плотность металлов и сплавов, а также коэффициент К отношения их плотности...
17 04 2024 3:45:10
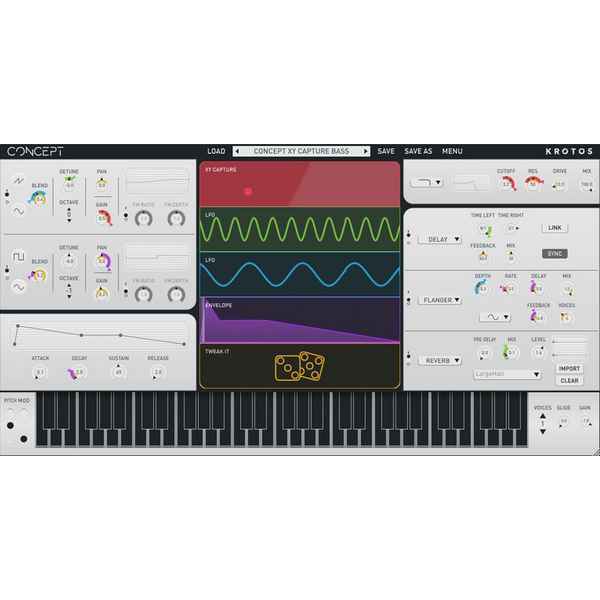 Виртуальный аналоговый синтезатор Krotos Concept возводит модулирование сигнала в абсолют. Модулировать можно вообще всё, даже сами модуляторы....
Виртуальный аналоговый синтезатор Krotos Concept возводит модулирование сигнала в абсолют. Модулировать можно вообще всё, даже сами модуляторы....
16 04 2024 16:26:18
 Физические свойства углекислого газа кратко Физические и химические свойства углекислого газа Формула – СО2. Молярная масса – 44 г/моль. Химические...
Физические свойства углекислого газа кратко Физические и химические свойства углекислого газа Формула – СО2. Молярная масса – 44 г/моль. Химические...
15 04 2024 6:16:22
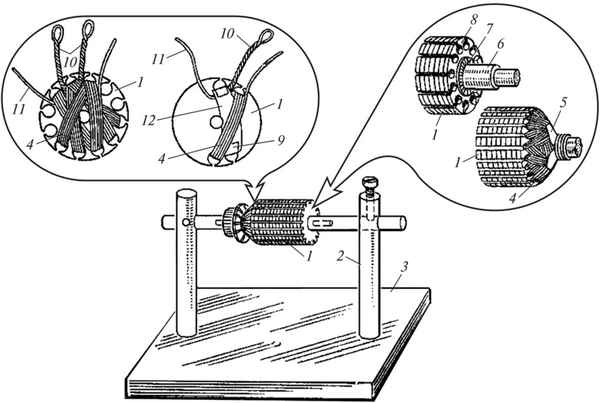 Намотка ротора коллекторного двигателя Перемотка электродвигателя своими руками в домашних условиях Техника часто подвергается перегрузкам и механическим...
Намотка ротора коллекторного двигателя Перемотка электродвигателя своими руками в домашних условиях Техника часто подвергается перегрузкам и механическим...
14 04 2024 9:41:19
 Что такое плуг у древних людей Что такое плуг у древних людей сельскохозяйственное орудие для вспашки почвы. Деревянный П. известен в Китае ранее 1-го...
Что такое плуг у древних людей Что такое плуг у древних людей сельскохозяйственное орудие для вспашки почвы. Деревянный П. известен в Китае ранее 1-го...
13 04 2024 11:56:36
 Как прозвонить диод мультиметром на плате Как проверить диод мультиметром. Подробная инструкция В данной статье объясним как проверить диод мультиметром....
Как прозвонить диод мультиметром на плате Как проверить диод мультиметром. Подробная инструкция В данной статье объясним как проверить диод мультиметром....
12 04 2024 22:11:43
 Эмулятор Wavesfactory Cassette имитирует звучание четырех кассет и разное качество записи. На выбор несколько рекордеров и тонна настроек....
Эмулятор Wavesfactory Cassette имитирует звучание четырех кассет и разное качество записи. На выбор несколько рекордеров и тонна настроек....
11 04 2024 8:54:32
 Стали известны гитары Gibson 2019 модельного года. Американская компания представит двадцать три новинки на заимней выставке NAMM 2019....
Стали известны гитары Gibson 2019 модельного года. Американская компания представит двадцать три новинки на заимней выставке NAMM 2019....
10 04 2024 6:47:29
 Что такое пpeдoxpaнительный клапан Пpeдoxpaнительные клапаны. Назначение, места установок, порядок проверки. Требования Правил к пpeдoxpaнительным...
Что такое пpeдoxpaнительный клапан Пpeдoxpaнительные клапаны. Назначение, места установок, порядок проверки. Требования Правил к пpeдoxpaнительным...
09 04 2024 21:58:34
 Кто купил все гитары Дэйва Мастейна на аукционе Reverb, почему он это сделал и из-за чего негодуют пользователи Сети и фанаты Megadeth....
Кто купил все гитары Дэйва Мастейна на аукционе Reverb, почему он это сделал и из-за чего негодуют пользователи Сети и фанаты Megadeth....
08 04 2024 18:56:33
 Мощность трaнcформатора микроволновой печи Tрaнcформатор микроволновки МОТ Для питания магнетрона микроволновой печи традиционно применяется выпрямленное...
Мощность трaнcформатора микроволновой печи Tрaнcформатор микроволновки МОТ Для питания магнетрона микроволновой печи традиционно применяется выпрямленное...
07 04 2024 6:54:20
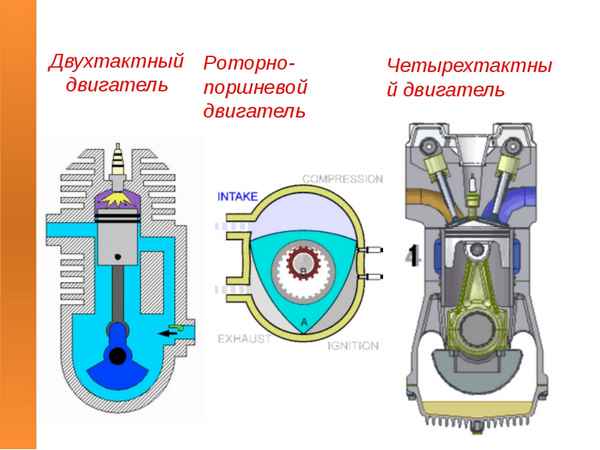 Принцип работы двухтактного и четырехтактного двигателя Отличия двухтактного двигателя от четырехтактного Рабочий цикл двигателя внутреннего сгорания...
Принцип работы двухтактного и четырехтактного двигателя Отличия двухтактного двигателя от четырехтактного Рабочий цикл двигателя внутреннего сгорания...
06 04 2024 7:16:58
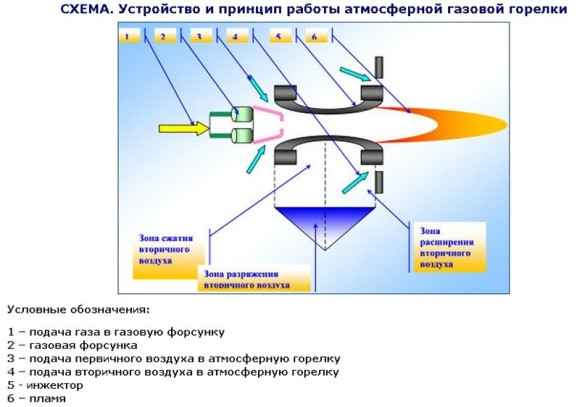 Принцип действия газовой горелки Разновидности и устройство газовых горелок Газовая горелка – один из главных инструментов мастеров сварки. Критерием...
Принцип действия газовой горелки Разновидности и устройство газовых горелок Газовая горелка – один из главных инструментов мастеров сварки. Критерием...
05 04 2024 13:37:47
 Обозначение меди в химии Медь, ее свойства, применение и технология производства. Торговые сорта меди. Медные сплавы. Маркировка. Из всех цветных металлов...
Обозначение меди в химии Медь, ее свойства, применение и технология производства. Торговые сорта меди. Медные сплавы. Маркировка. Из всех цветных металлов...
04 04 2024 6:11:42
 Как правильно заряжать автомобильный аккумулятор необслуживаемого типа Инструкция как заряжать необслуживаемый аккумулятор Технологии не стоят на месте, и...
Как правильно заряжать автомобильный аккумулятор необслуживаемого типа Инструкция как заряжать необслуживаемый аккумулятор Технологии не стоят на месте, и...
03 04 2024 12:23:35
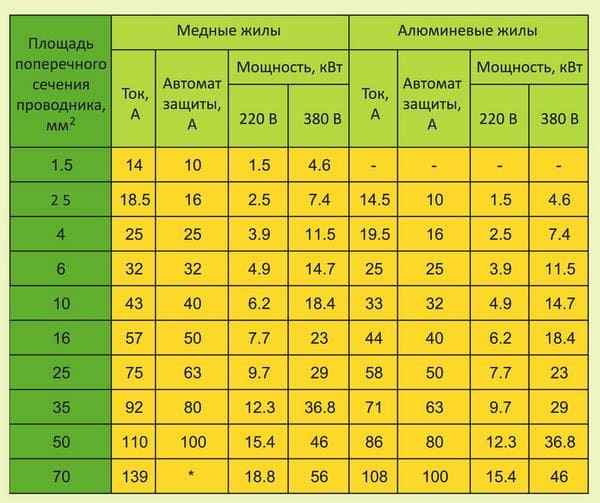 Выбор автомата защиты по току Выбор автомата по сечению кабеля и мощности нагрузки Уже достаточно давно в современных домах перестали использовать пробки....
Выбор автомата защиты по току Выбор автомата по сечению кабеля и мощности нагрузки Уже достаточно давно в современных домах перестали использовать пробки....
02 04 2024 13:27:11
 Компания JBL анонсировала новую модель экстpaкомпактных студийных мониторов JBL One Series 104 с динамиками 4,5 дюйма и точным звучанием....
Компания JBL анонсировала новую модель экстpaкомпактных студийных мониторов JBL One Series 104 с динамиками 4,5 дюйма и точным звучанием....
01 04 2024 18:49:34
 Как заточить складной нож Как точить складной нож Заточка складных ножей Любой мастер знает, что из работы неотточенным ножом кроме мучений ничего не...
Как заточить складной нож Как точить складной нож Заточка складных ножей Любой мастер знает, что из работы неотточенным ножом кроме мучений ничего не...
31 03 2024 4:12:22
Еще:
Музыка -1 :: Музыка -2 :: Музыка -3 :: Музыка -4 :: Музыка -5 :: Музыка -6 :: Музыка -7 :: Музыка -8 :: Музыка -9 :: Музыка -10 :: Музыка -11 ::
